nLab partial trace
Context
Linear algebra
linear algebra, higher linear algebra
Ingredients
Basic concepts
Theorems
(…)
Contents
Idea
A partial trace is a trace applied to (only) one factor in a tensor product.
The partial trace is generalized by traced monoidal categories. That is, a traced monoidal category is a monoidal category paired with an operation which behaves like the partial trace.
Definition
Let denote the category of finite-dimensional vector spaces over a field . The partial trace gives a compatible collection of linear maps
given by
where “” on the right denotes the usual trace.
Explicitly, the partial trace can also be defined as follows:
Let be an endomorphism. Let and be linear bases for and respectively. Then has a matrix representation where and relative to the basis of the space given by . Consider the sum
for over . This gives the matrix . The associated linear operator on is independent of the choice of bases and corresponds to the partial trace.
String diagram representations
Given vector spaces , or more generally, given objects in a traced monoidal category, we will often write the partial trace using string diagrams as follows:
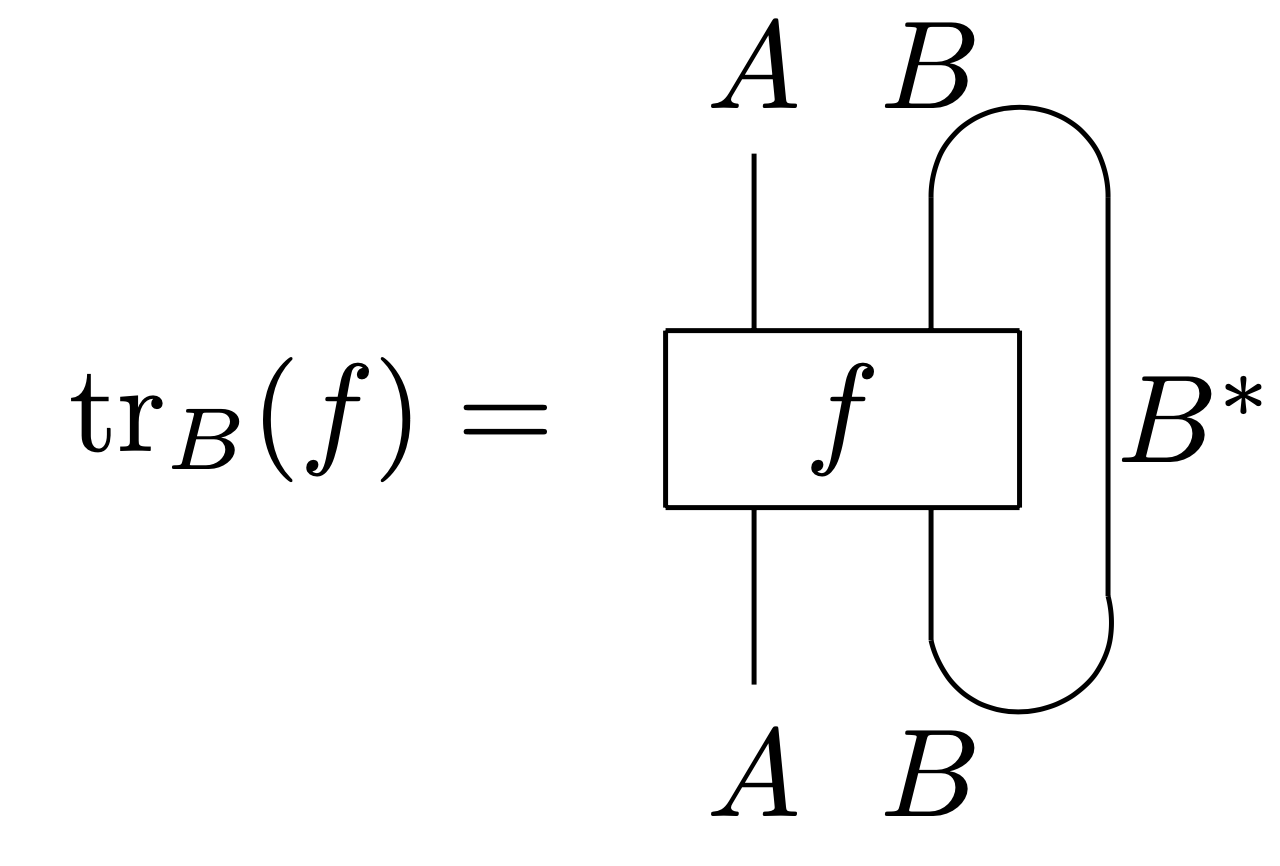
Considering as a pivotal category, this diagram is completely rigorous. To make sure this notation is consistent, we verify
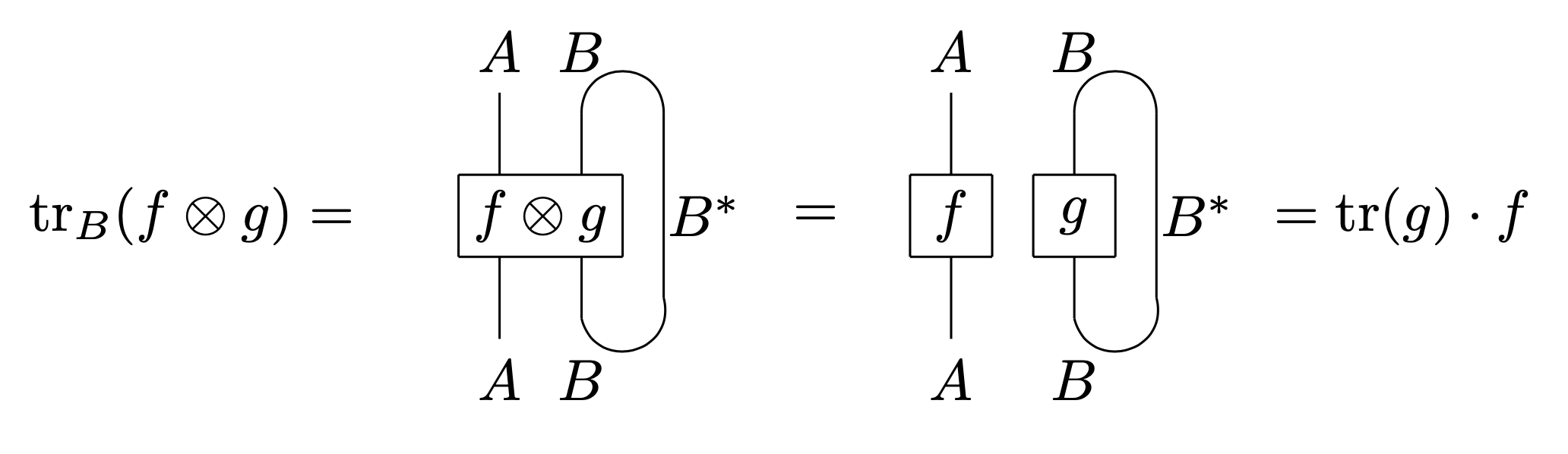
Additionally the closed loop can only be trace. This is because the axioms of a pivotal category we can move around the loop, so
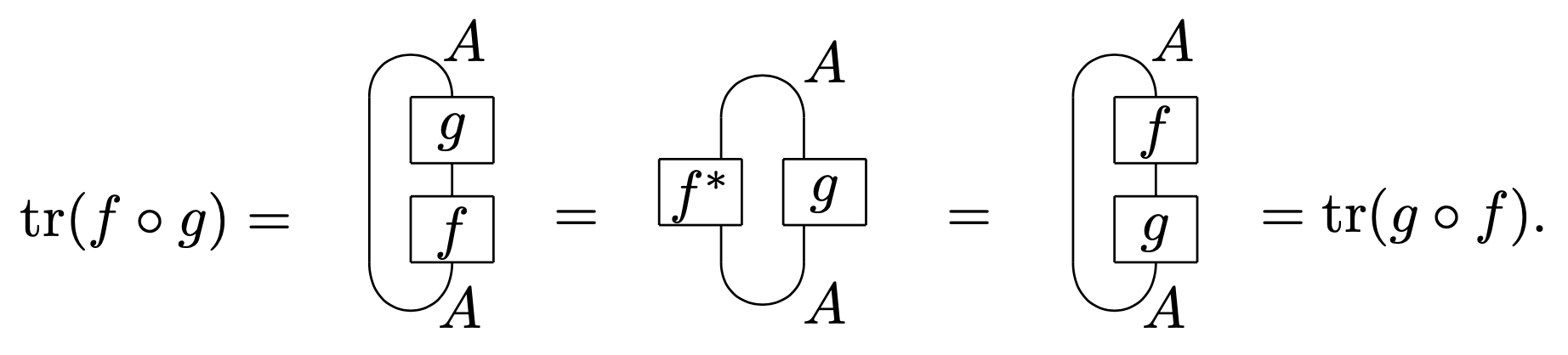
It is a standard fact from linear algebra that the trace is uniquely characterized by the fact that it is linear and acts the same on and for all .
Related concepts
Last revised on September 24, 2023 at 09:56:40. See the history of this page for a list of all contributions to it.